Machine Learning Notes I - Introduction & Math Review

SVD, MLE, Entropy

Authors

Affiliations

Published

April 1, 2025

All modern machine learning algorithms are just nearest neighbors. It’s only that the neural networks are telling you the space in which to compute the distance.

Linear Algebra

Woodbury Identity

(A + U C V)^{- 1} = A^{- 1} - A^{- 1} U (C^{- 1} + V A^{- 1} U) V^{- 1}

其中

A \in R^{n \times n}, C \in R^{k \times k}, k ≪ n

如果 $A$ 的逆很好算，那这样变换会大大降低计算量。

Matrix Derivatives

向量 / 标量

f (x + Δ) = f (x) + \frac{\partial f}{\partial x} Δ + o (‖ Δ ‖)

\nabla f = {(\frac{\partial f}{\partial x})}^{⊤}

所以假设说 $f : R^{n} \to R$ ，我们就应该有

\begin{aligned} \frac{\partial f}{\partial x} & = [\begin{array}{c} \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{1}} & \dots & \frac{\partial f}{\partial x_{n}} \end{array}] & \in R^{1 \times n} \\ \nabla f & = {(\frac{\partial f}{\partial x})}^{⊤} = [\begin{array}{c} \frac{\partial f}{\partial x_{1}} \\ \frac{\partial f}{\partial x_{1}} \\ ⋮ \\ \frac{\partial f}{\partial x_{n}} \end{array}] & \in R^{n} \end{aligned}

标量 / 矩阵

同样的，对于 $f : R^{m \times n} \to R$ ，我们有：

{(\frac{\partial f}{\partial X})}_{i j} = \frac{\partial f}{\partial X_{j i}}

酱紫

f (X + Δ) = f (X) + Tr (\frac{\partial f}{\partial X} Δ) + o (‖ Δ ‖)

Jacobian: 向量 / 向量

假设函数是 $z : R^{d} \to R^{k}$ ，我们想要有

z (x + Δ) = z (x) + J (z) Δ + o (‖ Δ ‖)

所以其实我们可以看成是 $z$ 的每行单独拆开来嘛，也就是

J (z) = \frac{\partial z}{\partial x} = [\begin{matrix} \frac{\partial z_{1}}{\partial x} \\ \frac{\partial z_{2}}{\partial x} \\ ⋮ \\ \frac{\partial z_{k}}{\partial x} \end{matrix}] = [\begin{matrix} \frac{\partial z_{1}}{\partial x_{1}} & \frac{\partial z_{1}}{\partial x_{2}} & \dots & \frac{\partial z_{1}}{\partial x_{d}} \\ \frac{\partial z_{2}}{\partial x_{1}} & \frac{\partial z_{2}}{\partial x_{2}} & \dots & \frac{\partial z_{2}}{\partial x_{d}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \frac{\partial z_{k}}{\partial x_{1}} & \frac{\partial z_{k}}{\partial x_{2}} & \dots & \frac{\partial z_{k}}{\partial x_{d}} \end{matrix}]

[J (z)]_{i j} = {(\frac{\partial z}{\partial x})}_{i j} = \frac{\partial z_{i}}{\partial x_{j}}

Hessian: 二阶导

对于函数 $f : R^{n} \to R$ ，我们想要求二阶导

\nabla f (x + Δ) = \nabla f (x) + \nabla^{2} f (x) Δ + o (‖ Δ ‖)

所以其实就是

H (f) = \nabla^{2} f (x) = [J (f (x))]^{⊤} = [\begin{matrix} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \dots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \dots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \dots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{matrix}]

Derivative Rules

我们先来算 $\frac{\partial}{\partial x} (A B)$ ，考虑到

\begin{aligned} {[\frac{\partial}{\partial x} (A B)]}_{i j} & = \frac{\partial}{\partial x} (A B)_{i j} = \frac{\partial}{\partial x} \sum_{k} A_{i k} B_{k j} \\ = \sum_{k} (\frac{\partial A_{i k}}{\partial x} B_{k j} + A_{i k} \frac{\partial B_{k j}}{\partial x}) \\ = \frac{\partial A}{\partial x} B + A \frac{\partial B}{\partial x} \end{aligned}

将 $A^{- 1} A = I$ 代入上式可以得到

\frac{\partial}{\partial x} A^{- 1} = - A^{- 1} \frac{\partial A}{\partial x} A^{- 1}

SVD

Notes

A = U Σ V^{⊤} = \sum_{i = 1}^{min {m, n}} σ_{i} u_{i} v_{i}^{⊤}

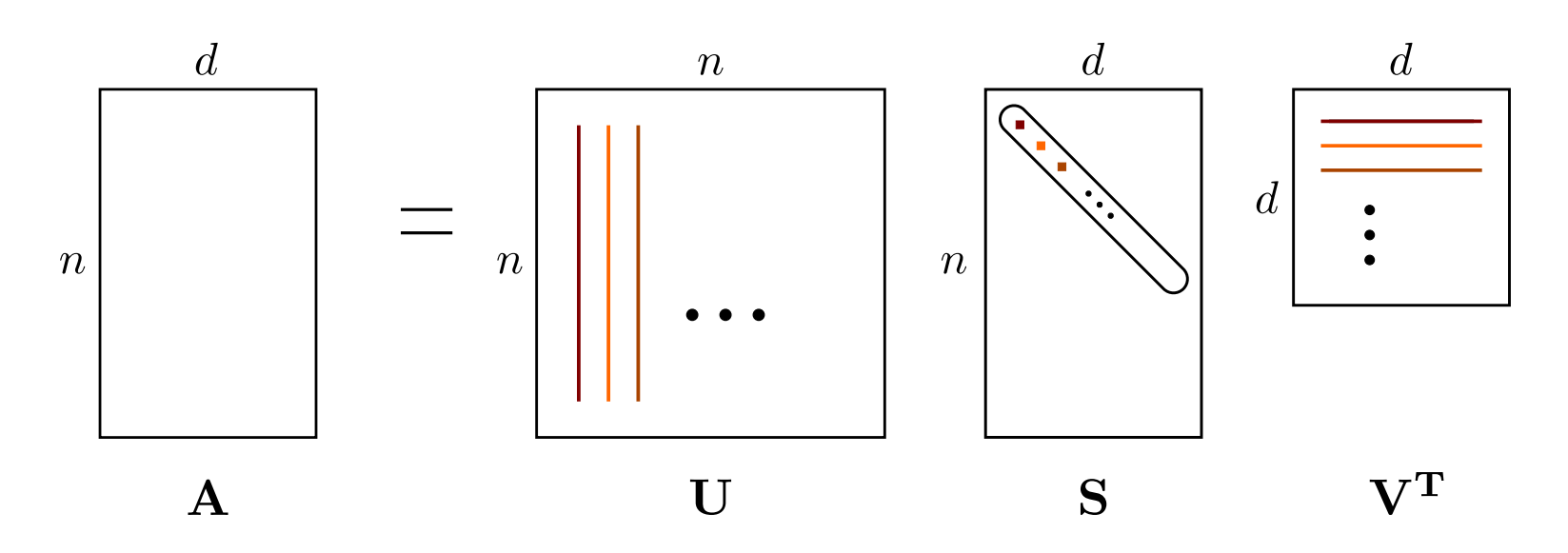
Compute largest $k$ singular values and vectors: $O (k m n)$ .

Approximation:

\hat{A} = \sum_{i = 1}^{k} σ_{i} u_{i} v_{i}^{⊤} = U_{k} Σ_{k} V_{k}^{⊤}

For all rank $k$ matrices $B$ :

‖ A - \hat{A} ‖_{F} \leq ‖ A - B ‖_{F}

Calculus of Variations

变分法中，我们考虑的是对于一个函数的函数 $F (f)$ ， $f$ 稍稍改变， $F$ 就会稍稍改变：

F [y (x) + ϵ η (x)] = F [y (x)] + ϵ \int \frac{δ F}{δ y (x)} η (x) d x + O (ϵ^{2})

假设

F [y] = \int G (y (x), y^{'} (x), x) d x

那么

\begin{aligned} \int \frac{δ F}{δ y (x)} η (x) d x & = \end{aligned}

Maximum Likelihood Estimation

Maximum likelihood estimation:

\hat{θ} = \arg max_{θ \in Θ} p (D ∣ θ)

Properties:

Consistency: more data, more accurate (but maybe biased).
Statistically efficient: least variance.
The value of $p (D ∣ θ_{MLE})$ is invariant to re-parameterization.

Entropy

要搞一个 “degree of surprise” 函数 $h (p (x))$ ，满足：

$h (p) \geq 0$ ;
$h (p) = 0 ⟺ p = 1$ ;
$x ⊥ y ⟺ h (p (x \land y)) = h (p (x)) + h (p (y))$ ;
$h (p_{1}) > h (p_{2}) ⟺ p_{1} < p_{2}$ .

根据 3 我们有

h (p_{1} p_{2}) = h (p_{1}) + h (p_{2})

如果我们令 $f (\log p) = h (p)$ 的话，我们有

f (\log p_{1} + \log p_{2}) = f (\log p_{1}) + f (\log p_{2})

所以 $f (p)$ 是一个线性函数。又因为 $f (0) = 0$ ，所以 $f (x) = - c \cdot x$ 。 $c > 0$ 因为 $f$ 要单调递减且非负。

所以

h (p (x)) = - c \cdot \log p (x)

通常我们取 $c = 1$ 或 $c = \frac{1}{\log 2}$ 。这边就不管了都写成 $- \log p (x)$ 了。

于是我们定义

H (x) = E [h (p (x))] = - \int p (x) \log p (x)

当然因为 entropy 是从物理来的，他也有一定物理意义。就是我们考虑有 $N$ 个东西， $k$ 个状态。第 $i$ 个状态有 $n_{i}$ 个。那么可能的排列数量为

W = \frac{N!}{\prod n_{i}!}

我们考虑定义 $H$ 为 $N \to \infty$ 时候的状态

\begin{aligned} H & = lim_{N \to \infty} \frac{1}{N} \log W = - lim_{N \to \infty} (\frac{n_{i}}{N_{i}}) \log (\frac{n_{i}}{N}) \end{aligned}

其中用到了 Stirling’s approximation

\log n! = n \log n - n + O (\log n)

那啥时候 $H$ 最大捏？