Game Theory | Fanyi Pu

Preferences

一些基础定义和概念

Consumption Space: $X\subseteq\mathbb{R}_+^n$

Preference Relation: $x\succsim y$ or $x\succeq y$, $x$ is as lease as good as $y$

Indifference: $x\sim y \Longleftrightarrow x\succsim y \land y\succsim x$

Strict Preference: $x\succ y \Longleftrightarrow x\succsim y \land x\nsim y$

常见的 Assumptions

Preference 这个概念挺大的，通常我们会带着一些 assumption 来研究。下面是一些常见的 assumption。

Rationality Assumption: completeness and transitivity。

这样不会陷入死循环和一些矛盾的情况。

反例：

剪刀石头布：$x\succ y\succ z\succ x$，无法做出最优选择
咖啡加糖：$c_1\sim c_{0.9}\sim c_{0.8}\sim\cdots\sim c_{0.1}\sim c_0$，但是$c_1\nsim c_0$。需要考虑一些心理的情况。

Convex Combination:

\[\alpha x+(1-\alpha)y, \alpha\in[0,1]\]

Convex Set:

\[\forall x, y\in X\ ,\forall\alpha\in[0, 1], \alpha x+(1-\alpha)y\in X\]

Convex Function:

\[f: X\to\mathbb{R}, \forall x, y\in X, \forall\alpha\in[0, 1], f(\alpha x+(1-\alpha)y)\le \alpha f(x)+(1-\alpha)f(y)\]

Convex 是笑脸，concave 是哭脸。

高维空间比大小的一些记号：

\[\begin{aligned} x\ge y&\Longleftrightarrow \forall i, x_i\ge y_i\\ x>y&\Longleftrightarrow x\ge y\land x\neq y\\ x\gg y&\Longleftrightarrow \forall i, x_i>y_i \end{aligned}\]

Strongly Monotone:

\[x>y\Longrightarrow f(x)>f(y)\]

Weakly Monotone:

\[x\gg y\Longrightarrow f(x)> f(y)\]

Locally Satisfied Preference:

\[\forall x\in X, \forall \epsilon>0, \exists y, \lVert x-y\rVert<\epsilon\land y\succsim x\]

旁边总有比他好的。

Weekly Monotone Preference:

\[x\gg y\Longrightarrow x\succ y\]

所有东西都来一点更好。

Strongly Monotone Preference:

\[x>y\Longrightarrow x\succ y\]

越多越好。

Convex Preference:

\[x\succsim z, y\succsim z\Longrightarrow\forall\alpha\in[0, 1], \alpha x+(1-\alpha)y\succsim z\]

Strictly Convex Preference:

\[x\succsim z, y\succsim z, y\neq x\Longrightarrow \forall\alpha\in(0, 1), \alpha x+(1-\alpha)y\succ z\]

我们称 $f$ 是 quasi-concave 的当且仅当

\[f(\lambda x+(1-\lambda)y)\le\max\{f(x), f(y)\}\]

Continuous Preference:

\[\forall n\in\mathbb{N}, x_n\succsim y_n, x_n\to x, y_n\to y\Longrightarrow x\succsim y\]

Utility Functions

我们定义一个 $u: X\to \mathbb{R}$ 使得

\[u(x)\ge u(y)\Longleftrightarrow x\succsim y\]

我们说是 $u$ represents $\succsim$。

这个 $u$ 就是 $\succsim$ 的 utility functions。

一个定理是 $\succsim$ 是 rational and continuous 的当且仅当存在一个连续的 $u$。

$\succsim$ is monotone $\Longleftrightarrow$ $u$ is monotone
$\succsim$ is convex $\Longleftrightarrow$ $u$ is quasi-concave

当然很显然地：

\[\begin{cases} x\sim y\Longleftrightarrow u(x)=u(y)\\ x\succ y\Longleftrightarrow u(x)>u(y) \end{cases}\]

Marginal Utility

\[\mathrm{MU}(x)=\frac{\partial u(x)}{\partial x}\]

一般比如说对钱，我们会有 $\mathrm{MU}(x)$ 是递减的。给的越多，多一块的价值越小。也就是 $u''(x)<0$。

Decision Making Under Uncertainty

Lotteries

在有 uncertainty 的情况下，用户做的决策是 lotteries，而不是确定的 goods。

A lottery is a vector $L = (x_1, p_1; x_2, p_2; \cdots; x_n, p_n)$. $x_i$ 是 realization，$p_i$ 是 probability。

对于某个 realization，我们有其 utility $u(x_i)$，然后我们定义整个 lottery 的 utility 为 $U(L) = \mathbb{E}[u(L)]$ (Von-Neumann Morgenstern Utility Function)。

很多时候我们会对 lotteries 做线性叠加，比如一些钱买定期，一些钱买股票。所以其实我们就是在一个 convex set 上做决策。

这时候问题就简化为我们有 $n$ 个 realizations $X = \{x_1, x_2, \cdots, x_n\}$，将这 $n$ 个 realizations 做线性组合，我们将这个 simplex 定义为 $\mathbb{L}(X)$，也就是：

\[\mathbb{L}(X) = \left\{(x_1, p_1; x_2, p_2; \cdots; x_n, p_n): p_i\ge 0, \sum_{i=1}^n p_i = 1\right\}\]

我们同样可以在 $\mathbb{L}(X)$ 上定义 $\succsim$，而 $\succsim$ 需要满足如下公理：

Completeness: $\forall L_1, L_2\in\mathbb{L}(X), L_1\succsim L_2\lor L_2\succsim L_1$
Transitivity: $L_1\succsim L_2, L_2\succsim L_3\Longrightarrow L_1\succsim L_3$
Continuity: $L_1\succsim L_2\succsim L_3\Longrightarrow \exists\alpha\in[0, 1], L_2\sim \alpha L_1+(1-\alpha)L_3$
Independence: $L_1\succsim L_2\Longrightarrow \forall \alpha\in[0, 1], \alpha L_1+(1-\alpha)L_3\succsim \alpha L_2+(1-\alpha)L_3$

Von Neumann–Morgenstern utility theorem: 上面四条同时 hold，等价于存在一个 $u$，并且任何可行的 $u'$ 都可以通过一个 affine transformation 得到：$u' = a+bu, b>0$。

St. Petersburg paradox

这个是用来展示为什么必须要用 $\mathbb{E}[u(L)]$ 而不是直接 $\mathbb{E}[L]$ 的例子。

假设有一个游戏，需要 1000 块钱。游戏是给你一个硬币你去抛，如果正面就给你一块钱继续抛，第二次正面两块钱，第三次四块钱，第 $n$ 次 $2^{n-1}$ 块钱，直到你抛到反面结束。

这个游戏是铁不会玩的，因为你回本概率挺低的。但是

\[\mathbb{E}[L] = \sum_{n=1}^\infty\frac{1}{2^n}\times 2^{n-1} = \infty\]

这也显示了人们对赌钱是 risk averse 的。

Risk Aversion

对于一个通过 $u$ 来进行选择的 agent，我们判断他是否喜欢 take risks：

Risk Averse: $u(\mathbb{E}[L])\ge \mathbb{E}[u(L)]$
Risk Neutral: $u(\mathbb{E}[L]) = \mathbb{E}[u(L)]$
Risk Loving: $u(\mathbb{E}[L])\le \mathbb{E}[u(L)]$

用 Jensen’s inequality 很好判断: For a convex function $f$, we have $f(\mathbb{E}[X])\le \mathbb{E}[f(X)]$.

对于一个 Risk Averse 的 agent，会有一个 $\mathrm{CE}$ 来表示他愿意用这么多钱来换取一个稳定的状态：

\[u(\mathbb{E}[L]-\mathrm{CE}) = \mathbb{E}[u(L)]\]

我们考虑把一个 agent 的对 risk 的态度量化地表示，我们考虑 $-u''(x)$ 的正负是个很好的指标。但如果 $v=a+bu$，那么 $-v''(x)\neq -u''(x)$，所以我们考虑：

\[R_A(x)=-\frac{u''(x)}{u'(x)}\]

我们将其称作 Arrow-Pratt Absolute Risk Aversion Coefficient，越大越 risk averse。

但是有时候钱越多我们就会越极端，所以我们考虑定义 Relative Risk Aversion：

\[R_R(x)=-x\cdot\frac{u''(x)}{u'(x)}\]

Allais Paradox

考虑四个 lotteries：

Lottery A: $\left(\$10^6, 11\%; \$0, 89\%\right)$
Lottery B: $\left(\$5\times 10^6, 10\%; \$0, 90\%\right)$
Lottery C: $\left(\$10^6, 100\%\right)$
Lottery D: $\left(\$5\times 10^6, 10\%; \$10^6, 89\%, \$0, 1\%\right)$

A 比 B，C 比 D。几乎大部分人会更喜欢 B 和 C。（虽然其实我上课的时候选了 B 和 D 呃呃呃）

我们令 $u(x)$ 表示获得 $x\times 10^6$ 块钱，于是我们有：

\[\begin{cases} u(1)\times 0.11 < u(5)\times 0.1\\ u(1)>u(5)\times 0.1+u(1)\times 0.89 \end{cases}\]

而下面一个式子化简一下能得到：

\[u(1)\times 0.11 > u(5)\times 0.1\]

两个式子是矛盾的。

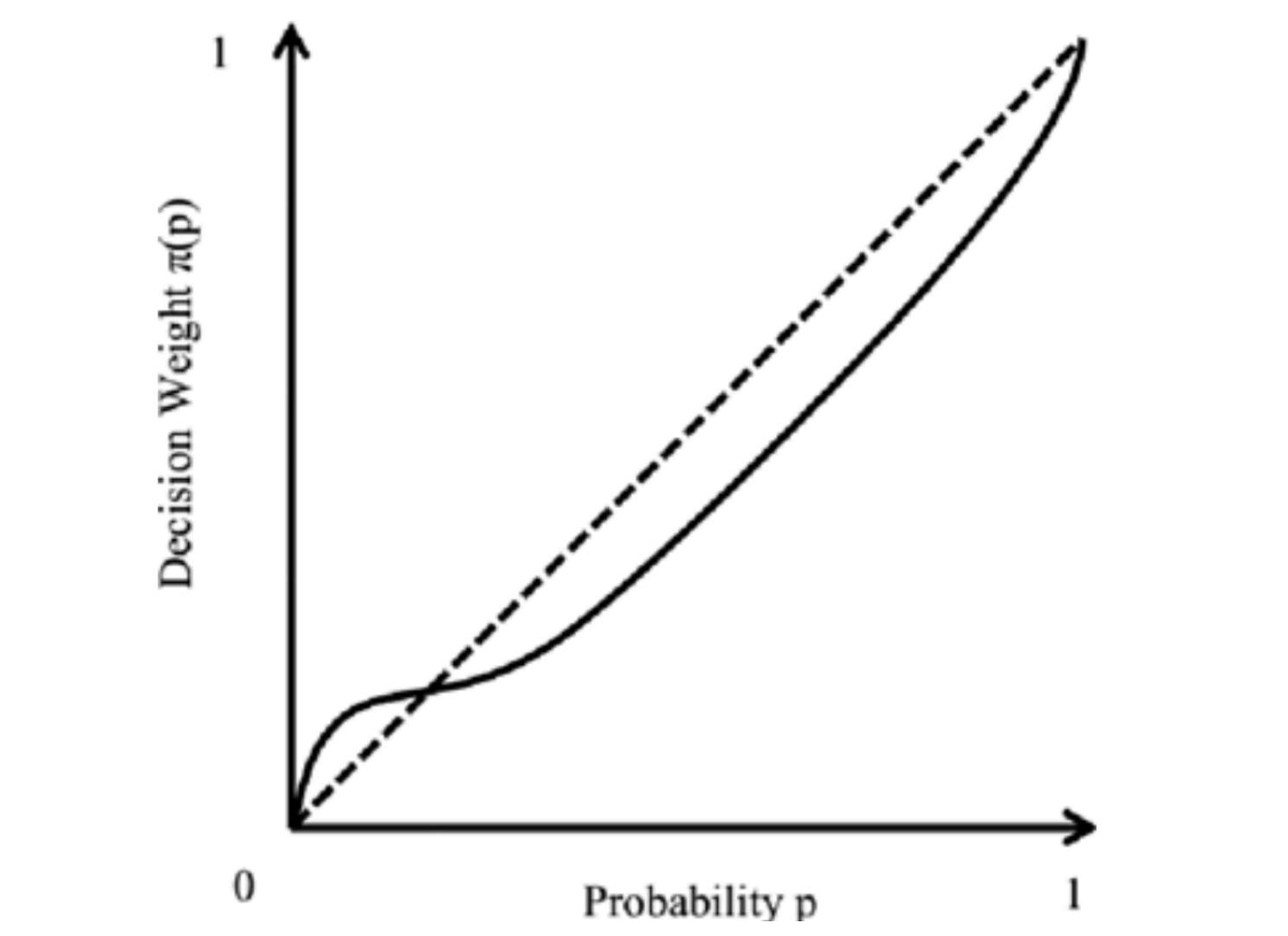
这让我们意识到其实在人真正考虑概率的时候，将“小概率发生”和“完全不发生”是分的很明确的。因为上面那个例子很多人时看到 D 项中有 $1\%$ 的概率拿不到钱而去选 C 项。解决方法是我们对概率需要加一个修正函数 $\pi(p)$，使得我们的 utility function 变为 $u(x)\times\pi(p)$。这个 $\pi$ 函数在 $p=0$ 的时候会有一个陡增。

Ambiguity Aversion

另一个叫 Ellsberg Paradox 的悖论，我们考虑现在有两个盒子，每个盒子有 100 个红球或黑球。第一个盒子有 50 红 50 黑，第二个盒子啥也不知道。

有四个选项：

A: 从第一个盒子里随机抽一个球，如果是红球，拿 100 块钱，否则拿 0 块钱
B: 从第一个盒子里随机抽一个球，如果是黑球，拿 100 块钱，否则拿 0 块钱
C: 从第二个盒子里随机抽一个球，如果是红球，拿 100 块钱，否则拿 0 块钱
D: 从第二个盒子里随机抽一个球，如果是黑球，拿 100 块钱，否则拿 0 块钱

很显然 $A\sim B, C\sim D$。尽管 A 和 B 加起来和 C 和 D 加起来是一样的，但大部分人会认为 $A\succ C, B\succ D$。

这是因为人们不喜欢不确定性，也就是 ambiguity aversion。

Definition of a Game

Actions and Preferences

接下来正是讨论 Game Theory 了。

之前我们考虑的都是一个人的选择，现在是多人的决策问题，也就是说我们要考虑别人的操作。

有 $N$ 个 agents，每个 agent 有一个 action set

\[\mathcal{S}_i = \{s_{1}^i, s_{2}^i, \cdots, s_{N_i}^i\}\]

当然后面好像也有很多是写成 $\mathcal{A}_i$ 的，反正看得懂就行。

A strategic game consists of

The players $\mathcal{N} = \{1, 2, \cdots, N\}$
Actions: $\mathcal{A}=\mathcal{A_1}\times\cdots\times\mathcal{A}_N$
Preferences: $\succsim_i$ for each player $i$
Outcomes

Information Sets and Strategies

The set of possible strategy profiles is

\[\mathcal{S} = \mathcal{S}_1\times \mathcal{S}_2\times\cdots\times \mathcal{S}_N\]

对于一个游戏，在玩的过程中，每个人都会有一个 information $H$，对于第 $i$ 个人所有可能的 information 集合我们记作 information sets $\mathscr{H}_i$。玩家只能看到 $H$ 以内的东西，其他的（比如 $H$ 以外别人的决策）他是看不见的。

对于第 $i$ 个玩家，假设现在有 information $H\in\mathscr{H}_i$，那么定义他可行的方案 $\mathcal{C}_i(H)\subseteq\mathcal{A}_i$（对于每个 $H$ 可行方案肯定是一样的，否则他就有更多 information 了），然后我们定义他的 strategy 为 $s_i: \mathscr{H}_i\to\mathcal{A}_i$ 并且 $s_i(H)\in\mathcal{C}_i(H)$。

最终综合每个人的选择，我们有一个 strategy profile:

\[s = (s_1, s_2, \cdots, s_N)\in \mathcal{S}\]

而很多时候我们会关注某个 player $i$ 的 strategy，我们一般会将 strategy profile 写作 $(s_i, s_{-i})$，其中 $s_{-i}$ 是除了 $i$ 以外的其他人的 strategy。

Payoff Functions

对于一个游戏，第 $i$ 个人选了决策 $s_i$，我们有 $s=(s_1, s_2, \cdots, s_N)\in\mathcal{S}$。

这样子我们可以定义第 $i$ 个人的 utility function 为 $u_i(s)$，我们也叫做 payoff function。

两个人的时候我们通常写成表格的形式：

	Rock	Paper	Scissors
Rock	$(0, 0)$	$(-1, 1)$	$(1, -1)$
Paper	$(1, -1)$	$(0, 0)$	$(-1, 1)$
Scissors	$(-1, 1)$	$(1, -1)$	$(0, 0)$

Strategy Form

我们定义一个 $\mathcal{I}$ 个人的 simple game 的 strategy / normal form 为：

\[\Gamma = \left<\mathcal{I}, \left\{S_i\right\}, \left\{u_i(\cdot)\right\}\right>\]

Pure Strategies and Mixed Strategies

Pure strategy 指的是一个人只能选一个 action，而 mixed strategy 指的是一个人可以通过概率分布选多个 actions。

假设 $P_1$ 选的概率为 $\boldsymbol{p}$，$P_2$ 选的为 $\boldsymbol{q}$。$P_1$ 的 payoff 为 $M$，那么我们有 $P_1$ 的 expected payoff：

\[U_1(\boldsymbol{p}, \boldsymbol{q}) = \sum_{i\in\mathcal{I}}\sum_{j\in\mathcal{J}}M^{(1)}_{ij}p_iq_j=p^{\top}M_1q\]

对于每个人策略一定在一个 simplex 上，我们定义其为 $\Delta(\mathcal{I})$ 和 $\Delta(\mathcal{J})$。

Zero-Sum Games

最先讨论的是零和博弈。也就是

\[\forall s\in \mathcal{S}, \sum_{i=1}^N u_i(s) = 0\]

你要获利的唯一方法是让别人变差。

对于双人的，我们可以在表中只写第一个人的 payoff：

	Rock	Paper	Scissors
Rock	$0$	$-1$	$1$
Paper	$1$	$0$	$-1$
Scissors	$-1$	$1$	$0$

这样子也就是 $P_1$ 要最大化 $P_2$ 要最小化。

如果一个游戏不是零和的，我们可以加一个人，让

\[u_{N+1}(a_1, a_2, \cdots, a_N) = -\sum_{i=1}^N u_i(a_1, a_2, \cdots, a_N)\]

这样子就变成了零和博弈。

Security Level

$\underline{v}$: $P_1$ 先来，然后他考虑 $P_2$ 的最优策略。

对于 pure strategies：

\[\underline{v} = \max_{s_1\in\mathcal{S}_1}\min_{s_2\in\mathcal{S}_2}u_1(s_1, s_2)\]

对于 mixed strategies：

\[\underline{v} = \max_{\boldsymbol{p}\in\Delta(\mathcal{I})}\min_{\boldsymbol{q}\in\Delta(\mathcal{J})}p^{\top}Mq\]

$\overline{v}$: $P_2$ 先来，然后他考虑 $P_1$ 的最优策略。

对于 pure strategies：

\[\overline{v} = \min_{s_2\in\mathcal{S}_2}\max_{s_1\in\mathcal{S}_1}u_2(s_1, s_2)\]

对于 mixed strategies：

\[\overline{v} = \min_{\boldsymbol{q}\in\Delta(\mathcal{J})}\max_{\boldsymbol{p}\in\Delta(\mathcal{I})}p^{\top}Mq\]

很显然后手肯定是占优的，因为他知道先手的信息，所以

\[\underline{v}\le \overline{v}\]

如果 $\underline{v} = \overline{v}$，我们定义 $v=\underline{v}=\overline{v}$ 为 the value of the game。

Maxmin and Minmax Strategies

对于 maxmin 和 minmax，我们考虑的是假设我们告诉对手我们的策略（包含概率），对手选择最优 pure strategy。对于一个 $n\times m$ 的矩阵 $U$：

\[\begin{aligned} \max\min(U)&=\max_{\boldsymbol{p}\in\Delta[n]}\min_{y\in[m]}\sum_{i\in\mathcal{n}}p_i\cdot U_{i, y}\\ \min\max(U)&=\min_{\boldsymbol{q}\in\Delta[m]}\max_{x\in[n]}\sum_{j\in\mathcal{m}}q_j\cdot U_{x, j} \end{aligned}\]

Von Neumann’s Minimax Theorem: 对于零和博弈

\[\max\min(U) = \min\max(U)\]

Dominant Strategies

Strictly Dominant Strategies

对于一个 player，如果不管对方怎么做决策，他做某个决策一定是最优的，那这个决策就是 strictly dominant 的。

A strategy $s_i\in \mathcal{S}_i$ is strictly dominant for player $i$ if

\[\forall s_{-i}\in\mathcal{S}_{-i}, \forall s_i'\in\mathcal{S}_i, u_i(s_i, s_{-i})>u_i(s_i', s_{-i})\]

Strictly Dominated Strategies

我们说一个 strategy 是 strictly dominated 的，如果存在另一个 strategy 使得不管对方怎么做，这个 strategy 都比他好。换句话说，就是这个 strategy 一定不会被选。

A strategy $s_i\in \mathcal{S}_i$ is strictly dominated for player $i$ if

\[\exists s_i'\in\mathcal{S}_i, \forall s_{-i}\in\mathcal{S}_{-i}, u_i(s_i', s_{-i})>u_i(s_i, s_{-i})\]

Weakly Dominated Strategies

A strategy $s_i\in \mathcal{S}_i$ is weakly dominated for player $i$ if

\[\exists s_i'\in\mathcal{S}_i, \forall s_{-i}\in\mathcal{S}_{-i}, u_i(s_i', s_{-i})\ge u_i(s_i, s_{-i})\]

Iterated Elimination of Strictly Dominated Strategies

Strictly dominated strategies 一定不会被选，所以我们可以直接把这个策略去掉。然后我们就可以不断找每个人的 strictly dominated strategies，然后去掉来简化游戏。

不能用 weekly dominated strategies，因为这些策略还是有可能会被选的。

Strictly Dominated Strategies in Mixed Strategies

有时候尽管 pure strategy 不存在 strictly dominated strategies，考虑 mixed strategies 时可能会存在。

比如说

	L	R
U	$(10, 1)$	$(0, 0)$
M	$(4, 2)$	$(4, 1)$
D	$(0, 5)$	$(10, 2)$

这玩意儿 $M$ 是被 strictly dominated by $\frac{1}{2}U+\frac{1}{2}D$ 的。

我们说一个 mixed strategy $\sigma_i$ 是 strictly dominated 的，当且仅当存在 $\sigma_i'$ 使得

\[\forall\sigma_{-i}, u_i(\sigma_i', \sigma_{-i})>u_i(\sigma_i, \sigma_{-i})\]

移项然后展开：

\[u_i(\sigma_i', \sigma_{-i})-u_i(\sigma_i, \sigma_{-i})=\sum_{-i\in s_{-i}}\left[\prod_{k\neq i}\sigma_{k}(s_k)\right]\left[u_i(\sigma'_i, s_{-i})-u_i(\sigma_i, s_{-i})\right]>0\]

我们考虑这个式子，如果所有的 $u_i(\sigma'_i, s_{-i})-u_i(\sigma_i, s_{-i})>0$ 的话，很显然整个式子是正的，如果其中有一个小于 $0$，我们就让这一项前面的 $\sigma_k(s_k)=1$，其他都变成 $0$，这样整个式子就小于 $0$ 了。

于是乎对于一个 $\sigma_i$，我们只要 check 所有的 pure strategies 就可以。

Knowledge

Mutual Knowledge: 如果大家都知道某个 knowledge，那么这个 knowledge 是 mutual knowledge。

Common Knowledge: 如果任意一个 player 序列 $i_1, i_2, \cdots, i_k$，我们有 $i_1$ 知道 $i_2$ 知道 $\cdots$ 知道 $i_k$ 知道某个 knowledge，那么我们说这个 knowledge 是 common knowledge。

很显然 common knowledge 是 mutual knowledge。

假设人从左到右是 $A, B, C$，$A$ 不知道 $A$ 的帽子颜色。我们现在假定 player 序列是 $A, B, C$。对于 $A$ 来说，假设 $A$ 的帽子颜色是红的，那么 $B$ 就能看到俩红，那他就能知道 $C$ 肯定能看到至少一红。但是如果 $A$ 的帽子不是红色的，那么 $B$ 只能看到一红，他就不能确定 $C$ 是否能看到红色了。这导致了这道题不是 common knowledge。

Nash Equilibrium

Best Response

We say that a strategy $\sigma_i$ is a best response to $\sigma_{-i}$ if

\[\forall\sigma'_i\in\Delta(\mathcal{S}_i), u_i(\sigma_i, \sigma_{-i})\ge u_i(\sigma'_i, \sigma_{-i})\]

Best response correspondence:

\[b_i(\sigma_{-i})=\left\{\sigma_i\in\Delta(\mathcal{S}_i): \forall \sigma_i'\in\Delta(\mathcal{S}_i), u_i(\sigma_i, \sigma_{-i})\ge u_i(\sigma_i', \sigma_{-i})\right\}\]

Nash Equilibrium in Pure Strategies

每个人都是 best response 的策略。

A strategy profile $s=(s_1, \cdots, s_\mathcal{I})$ constitutes a Nash equilibrium of a game $\Gamma=\left[\mathcal{I}, \left\{S_i\right\}, \left\{u_i(\cdot)\right\}\right]$ if for every $i=1, \cdots, \mathcal{I}$,

\[u_i(s_i, s_{-i})\ge u_i(s_i', s_{-i})\]

for all $s_i'\in S_i$.

Nash Equilibrium in Mixed Strategies

和 pure strategies 的定义是一样的，对于游戏 $\Gamma=\left[\mathcal{I}, \left\{\Delta(\mathcal{S}_i)\right\}, \left\{u_i(\cdot)\right\}\right]$, 我们有 $\sigma = (\sigma_1, \cdots, \sigma_\mathcal{I})$ 是 Nash equilibrium if for every $i=1, \cdots, \mathcal{I}$,

\[u_i(\sigma_i, \sigma_{-i})\ge u_i(\sigma_i', \sigma_{-i})\]

for all $\sigma_i'\in\Delta(\mathcal{S}_i)$.

其实也就是

\[\forall i, \sigma_i\in b_i(\sigma_{-i})\]

所以直觉上来讲其实就是这些 correspondence 的交集。

比如说这个游戏：

	Bach ($\mathscr{B}_2$)	Stravinsky ($\mathscr{S}_2$)
Bach ($\mathscr{B}_1$)	$(10, 5)$	$(0, 0)$
Stravinsky ($\mathscr{S}_1$)	$(0, 0)$	$(5, 10)$

我们有对于 $P_1$：

\[\mathscr{B}_1\succsim\mathscr{S}_1\Longleftrightarrow p(\mathscr{B}_2)\ge\frac{1}{3}\]

同理，对称地对于 $P_2$：

\[\mathscr{B}_2\succsim\mathscr{S}_2\Longleftrightarrow p(\mathscr{B}_1)\ge\frac{2}{3}\]

画出图：

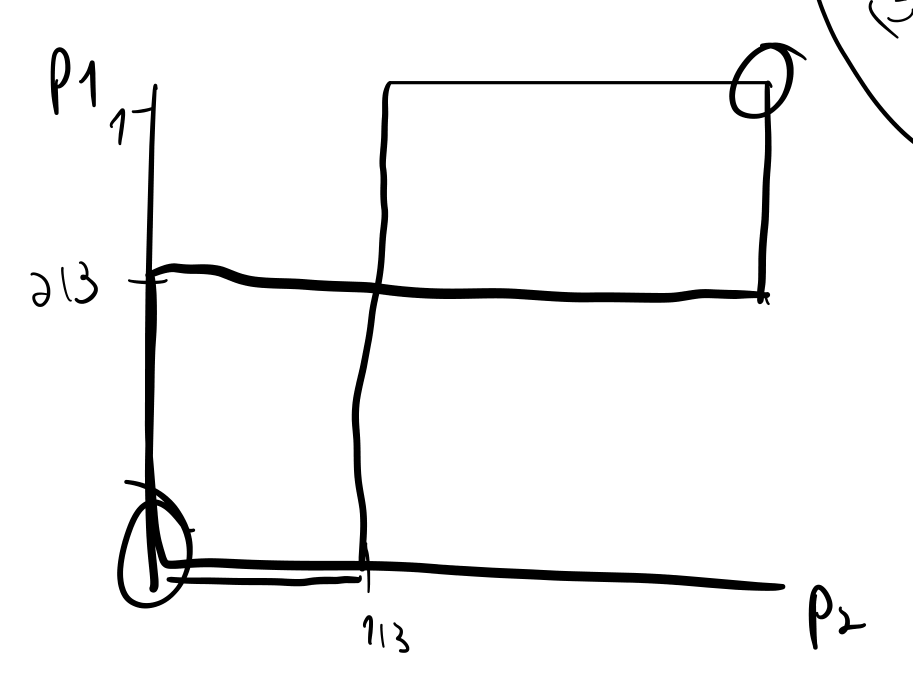
交点为 $(0, 0), \left(\frac{1}{3}, \frac{2}{3}\right), (1, 1)$，所以这三个点是 Nash equilibrium。

Checking for Nash Equilibrium

我们考虑游戏 $\Gamma=\left[\mathcal{I}, \left\{\Delta(\mathcal{S}_i)\right\}, \left\{u_i(\cdot)\right\}\right]$。对于一个 $\sigma=(\sigma_1, \cdots, \sigma_\mathcal{I})$，我们定义 $\mathcal{S}_i^+\subseteq\mathcal{S}_i$：

\[\mathcal{S}_i^+=\left\{s_j\in\mathcal{S}_i: \sigma_{i,j}>0\right\}\]

也就是这个人有可能执行这个操作。

于是乎一个 $\sigma$ 要满足他是 Nash equilibrium 当且仅当对于 $i=1, \cdots, \mathcal{I}$：

$u_i(s_i, \sigma_{-i})=u_i(s_i', \sigma_{-i})$ for all $s_i, s_i'\in\mathcal{S}_i^+$
$u_i(s_i, \sigma_{-i})\ge u_i(s_i', \sigma_{-i})$ for all $s_i\in\mathcal{S}_i^+$ and $s_i'\in\mathcal{S}_i\setminus\mathcal{S}_i^+$

大概就是，对于我来说，我知道别人有一个 mixed strategy，而我出的这个 mixed strategy 中的任何一种可能性都是一样优的（否则我就不要他了），而我不选的那几个操作一定不会更优（否则我肯定会增加它的概率）。如果对于每个人来说都是这样，那么就达到了一种均衡。

Existence of Nash Equilibrium

A Nash equilibrium exists in game $\Gamma=\left[\mathcal{I}, \left\{\mathcal{S}_i\right\}, \left\{u_i(\cdot)\right\}\right]$ if for all $i=1, \cdots, \mathcal{I}$:

$\mathcal{S}_i$ is a nonempty, convex, and compact subset of some Euclidean space $\mathbb{R}^M$;
$u_i(s_1, \cdots, s_\mathcal{I})$ is continuous in $(s_1, \cdots, s_\mathcal{I})$ and quasi-concave in $s_i$.

考虑到当 $\mathcal{S}$ 有限的时候，$\Delta(\mathcal{S})$ 满足了 nonempty, convex, compact 三个条件，而且 $u_i$ 也是 continuous 和 quasi-concave 的。所以我们说对于 mixed strategies game $\Gamma=\left[\mathcal{I}, \left\{\Delta(\mathcal{S}_i)\right\}, \left\{u_i(\cdot)\right\}\right]$，如果 $\mathcal{S}_i$ 是有限的，那么 Nash equilibrium 一定存在。

Correlated Equilibria

前面我们考虑 $\sigma_i$ 都是独立的。但在现实生活中，一些信息是共享的，导致我们的策略是相关的。

比如说红绿灯，大家会看到信号灯的信息来做出决策。

这时候我们就要定义：

\[U_i(\sigma_1, \cdots, \sigma_\mathcal{I})=\sum_{s}\mathbb{P}[s_1, \cdots, s_\mathcal{I}]u_i(s_1, \cdots, s_\mathcal{I})\]

而这时候我们的 strategy 概率就应该是定义在 $\mathcal{S}=S_1\times\cdots\times S_\mathcal{I}$ 上了，也就是描述 NE 需要考虑 joint distribution。

The Oddness Theorem

一个神奇的结论是在大部分情况下，一个游戏一定有奇数个 NE。

严谨的说，拥有偶数个 NE 的游戏所构成的集合 Lebesgue measure 为 $0$。

比如说有一个游戏：

	L	R
U	$(a_1, a_2)$	$(b_1, b_2)$
D	$(c_1, c_2)$	$(d_1, d_2)$

那么我们对于任意 $\epsilon>0$，存在 $0\le \epsilon_1, \cdots, \epsilon_8\le \epsilon$ 使得游戏：

	L	R
U	$(a_1+\epsilon_1, a_2+\epsilon_2)$	$(b_1+\epsilon_3, b_2+\epsilon_4)$
D	$(c_1+\epsilon_5, c_2+\epsilon_6)$	$(d_1+\epsilon_7, d_2+\epsilon_8)$

拥有奇数个 NE。

证明没有详细地讲，只说了个大概的思路。主要是考虑一个 $f: X\to X$ 的连续函数，不动点在大部分情况下有奇数个。除非与 $y=x$ 相切或者端点在 $(x, x)$ 上，这种情况下稍稍移动一下函数就可以了。

Welfare / Optimality

很多时候我们需要知道什么是“好的”，因为有时候 Nash equilibrium 并不是最优的。

最直观的方法是定义一个函数来表示整个社会的 welfare。我们定义 social welfare function 为

\[\mathcal{W}(x_1, \cdots, x_\mathcal{I})=\sum_{i=1}^\mathcal{I}\alpha_i u_i(x_i, x_{-i})\]

但这样做有两个很显然的问题：

谁来定义 $\alpha_i$？
是否所有人都能 accept 这个定义？

所以我们下面引出 Pareto Optimality。

Pareto Optimality

假设我们有两个 agents 和两种物品进行分配，第一个物品有 $A$ 个，第二个物品有 $B$ 个。那么我们可以定义 allocation 为：

\[\left((x_1^a, x_2^a), (x_1^b, x_2^b)\right)\]

而物品的数量有限，所以：

\[\begin{cases} x_1^a+x_1^b=A\\ x_2^a+x_2^b=B \end{cases}\]

我们定义一个 Pareto Improvement $\left((y_1^a, y_2^a), (y_1^b, y_2^b)\right)$ 满足：

\[\begin{bmatrix} u_a(y_1^a, y_2^a)\\ u_b(y_1^b, y_2^b) \end{bmatrix}> \begin{bmatrix} u_a(x_1^a, x_2^a)\\ u_b(x_1^b, x_2^b) \end{bmatrix}\]

其中的 $>$ 指的是有一个大于其余大于等于。

如果一个 allocation 没有 Pareto Improvement，那么我们称其为 Pareto Optimal。

然而 Pareto Optimal 也不一定是 fair 的，但是他是 bare minimum，也就是说如果不是 Pareto Optimal，那么我们应该做出改进。

上课提到了一个叫 laissez-fairez 的名词，其实就是自由放任。让市场自由调节来达到一个 Pareto Optimal 的状态。

Mechanism / Market Design

另一种让社会达到最优状态的方法叫 mechanism design，也叫 reverse game theory。我们通过设计和修改游戏机制来打到社会的最优性。

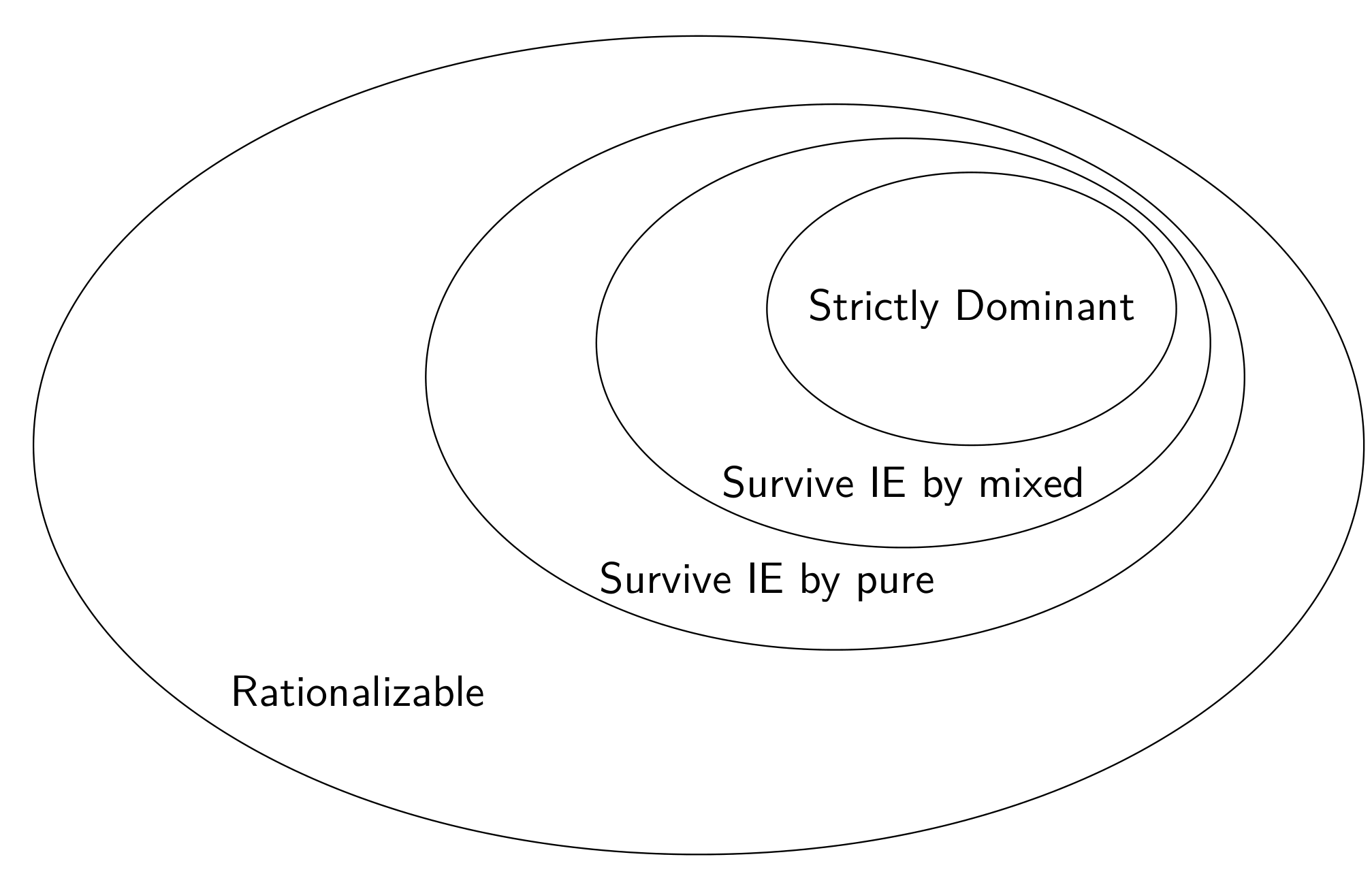
Rationalizable Strategies

我们考虑一个游戏，如果对方做出某个选择，我们会做出相应的 best response。但是有些策略不管对方选了什么，我们都不可能作为 best response 去选择，我们把这种策略叫做 NBR（never best response）。

那很显然 NBR 是可以忽略的，所以我们就重复在游戏中删除 NBR，直到没有 NBR 为止。

最终剩下来的策略就是 rationalizable strategies。

如果最终只剩了一个，那么我们说这个游戏是 dominance solvable 的。

很显然 NE 肯定是 rationalizable 的，因为如果他不是 rationalizable，那肯定在某一次删除的时候被定义为 NBR 了，而那个 best response 肯定比这个好。

但是 rationalizable 不一定是 NE 的，比如说 Matching Pennies：

	Heads	Tails
Heads	$(1, -1)$	$(-1, 1)$
Tails	$(-1, 1)$	$(1, -1)$

当然，NBR 也可能不是 strictly dominated by pure 的：

	X	Y
A	$(2, 1)$	$(0, 0)$
B	$(0, 1)$	$(2, 0)$
C	$(1, 1)$	$(1, 2)$

尽管我们考虑 pure strategies，$b_1(X)=\{A\}, b_1(Y)=\{B\}$，$C$ 是不会被选的。

Games with Trembling Hands

Trembling Hand Perfect Equilibrium

有时候我们做选择会手抖出错。也就其实是我们在选操作 $i$ 的时候，我们其实选的是一个概率分布 $\sigma_i$。

We say that a strategy profile $\sigma$ is a trembling-hand perfect Nash Equilibrium if it can be approximated by a sequence of totally mixed strategy profiles for each player. 其中的 totally mixed 指的是所有概率都大于 $0$。也就是说，对于一个 pure strategy，稍稍扰动一下也是没有问题的。

就比如下面这个例子：

	U	D
U	$(1, 1)$	$(0, -3)$
D	$(-3, 0)$	$(0, 0)$

$(D, D)$ 是 NE 但不是 THNE，因为如果稍微扰动一下，变成 $((\epsilon_1, 1-\epsilon_1), (\epsilon_2, 1-\epsilon_2))$，这时候是不如 $((1-\epsilon_1, \epsilon_1), (\epsilon_2, 1-\epsilon_2))$ 的。也就是说，在有 trembling hand 的情况下，$P_1$ 和 $P_2$ 其实会考虑换到 $U$。

Evolutionary Stable

当然根据这个定义，所有 totally mixed strategies 都是 THNE 的。但是我们可以沿用这个 idea 来定义和 “stability”。我们把一个 NE 扰动一下，如果还是 NE，那么我们就说这个 NE 是 stable 的。我们定义这个东西叫做 evolutionary stable。

A mixed strategy profile $\sigma^*$ is Evolutionary Stable if:

$u_i(\sigma_i^*, \sigma_{-i}^*)\ge u_i(\sigma_i, \sigma_{-i}^*)$ for all $i$ and $\sigma_i\in\Delta(\mathcal{S}_i)$
if $u_i(\sigma_i^*, \sigma_{-i}^*)=u_i(\sigma_i, \sigma_{-i}^*)$, then $u_i(\sigma_i^*, \sigma_{-i})>u_i(\sigma_i, \sigma_{-i})$

	Rock	Paper	Scissors
Rock	\((0, 0)\)	\((-1, 1)\)	\((1, -1)\)
Paper	\((1, -1)\)	\((0, 0)\)	\((-1, 1)\)
Scissors	\((-1, 1)\)	\((1, -1)\)	\((0, 0)\)

	Rock	Paper	Scissors
Rock	\(0\)	\(-1\)	\(1\)
Paper	\(1\)	\(0\)	\(-1\)
Scissors	\(-1\)	\(1\)	\(0\)

	L	R
U	\((10, 1)\)	\((0, 0)\)
M	\((4, 2)\)	\((4, 1)\)
D	\((0, 5)\)	\((10, 2)\)

	Bach (\(\mathscr{B}_2\))	Stravinsky (\(\mathscr{S}_2\))
Bach (\(\mathscr{B}_1\))	\((10, 5)\)	\((0, 0)\)
Stravinsky (\(\mathscr{S}_1\))	\((0, 0)\)	\((5, 10)\)

	L	R
U	\((a_1, a_2)\)	\((b_1, b_2)\)
D	\((c_1, c_2)\)	\((d_1, d_2)\)

	L	R
U	\((a_1+\epsilon_1, a_2+\epsilon_2)\)	\((b_1+\epsilon_3, b_2+\epsilon_4)\)
D	\((c_1+\epsilon_5, c_2+\epsilon_6)\)	\((d_1+\epsilon_7, d_2+\epsilon_8)\)