Machine Learning
Lecture 1: Introduction and Logistics
Some ideas
All modern machine learning algorithms are just nearest neighbors. It’s only that the neural networks are telling you the space in which to compute the distance.
Math Review
SVD
\[A = U \Sigma V^\top=\sum_{i=1}^{\min\{m, n\}}\sigma_i u_i v_i^\top\]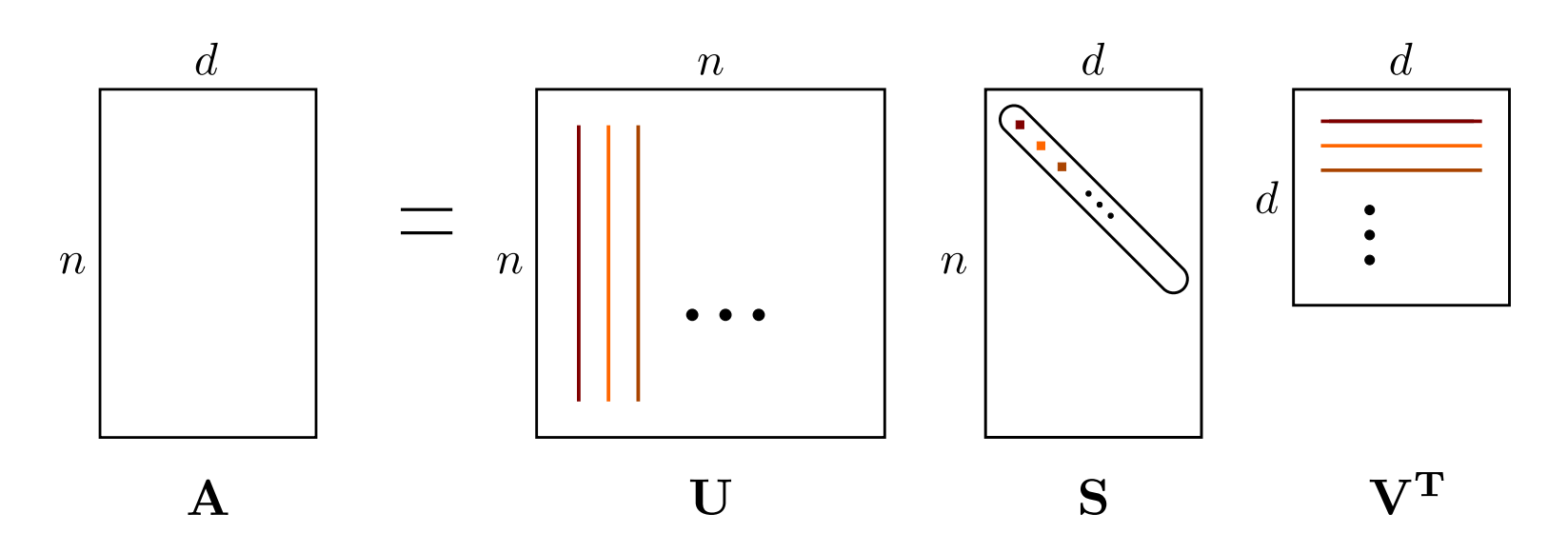
Compute largest \(k\) singular values and vectors: \(\mathcal{O}(kmn)\).
Approximation:
\[\hat{A} = \sum_{i=1}^{k}\sigma_i u_i v_i^\top = U_k \Sigma_k V_k^\top\]For all rank \(k\) matrices \(B\):
\[\|A - \hat{A}\|_F \le \|A - B\|_F\]Lecture 2: Maximum Likelihood Estimation
Discussed in my other notes.
Maximum likelihood estimation:
\[\hat{\theta} = \arg\max_{\theta\in\Theta} p(D\mid\theta)\]Properties:
- Consistency: more data, more accurate (but maybe biased).
- Statistically efficient: least variance.
- The value of \(p(D\mid\theta_{\text{MLE})\) is invariant to re-parameterization.